The question is: what is geometric intuition for the identity $\operatorname{Var}(X + Y) = \operatorname{Var}(X - Y)$ given that $X$ and $Y$ are independent?

To interpret this identity geometrically, it is helpful to view $\operatorname{Var}(X + Y)$ and $\operatorname{Var}(X - Y)$ as norms in the Hilbert space $L^2(\Omega, \mathscr{F}, P)$ equipped with inner product $\langle X, Y \rangle = E[XY]$.

To this end, write $\operatorname{Var}(X + Y)$ and $\operatorname{Var}(X - Y)$ as $$ \begin{align*} & \operatorname{Var}(X + Y) = E{[(X - \mu_X) + (Y - \mu_Y)]^2} = \|(X - \mu_X) + (Y - \mu_Y)\|^2, \\ & \operatorname{Var}(X - Y) = E{[(X - \mu_X) - (Y - \mu_Y)]^2} = \|(X - \mu_X) - (Y - \mu_Y)\|^2. \end{align*} $$

Therefore, by viewing $X - \mu_X$ and $Y - \mu_Y$ as two vectors in $L^2(\Omega, \mathscr{F}, P)$, $\operatorname{Var}(X + Y)$ and $\operatorname{Var}(X - Y)$ are squared lengths of the blue diagonal and the red diagonal in the parallelogram below respectively.

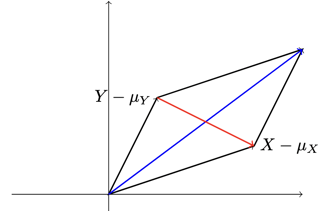
When $X$ and $Y$ are independent, $X - \mu_X$ and $Y - \mu_Y$ are clearly independent too, which means that $X - \mu_X$ and $Y - \mu_Y$ are orthogonal. That is, the parallelogram in the above diagram becomes a rectangle as shown below.

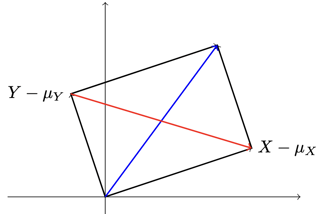
As diagonals in a rectangle are of the same length, we obtain $\operatorname{Var}(X + Y) = \operatorname{Var}(X - Y)$ geometrically.