The problem is posted on CrossValidated by a Spanish professor. It is stated as:

Suppose $(X, Y, Z) \sim f(x, y, z) = \frac{1}{3}(x + 2y + 3z), 0 < x, y, z < 1$ and $S = X + Y + Z$. Prove that $E[Y \mid S] = \frac{S}{3}$.

When the form of $E[Y \mid S]$ is given

Provided the answer is $E[Y \mid S] = \frac{S}{3}$, it suffices to show that $$ \begin{align*} \int_{S \leq s} Y dP = \int_{S \leq s} \frac{1}{3}SdP, \end{align*} $$ which, by the change-of-variable formula, is $$ \begin{align*} \iiint_V g(x, y, z)dxdydz = 0, \tag{1} \end{align*} $$ where $$ \begin{align*} & g(x, y, z) = (2y - x - z)(x + 2y + 3z), \\ & V = \{(x, y, z): 0 < x, y, z < 1, x + y + z \leq s\}. \end{align*} $$

Depending on whether $s \in (0, 1]$ or $s \in (1, 2)$ or $s \in [2, 3)$, $V$ has different forms, resulting different difficulty levels of the integral evaluation.

After converting the triple integral in $(1)$ to an iterative integral, we could resort to software to finish the mundane evaluation task (e.g., using Mathematica or Python, here I used the sympy package in Python to help me finish the work).

Case 1. $s \in (0, 1]$. In this case, the projection of $V$ onto the $x$-$y$ plane is $$ \begin{align*} \Delta = \{(x, y): 0 \leq y \leq s - x, 0 \leq x \leq s\}. \end{align*} $$

The visualization of $V$ and $\Delta$ is shown in the figure below:

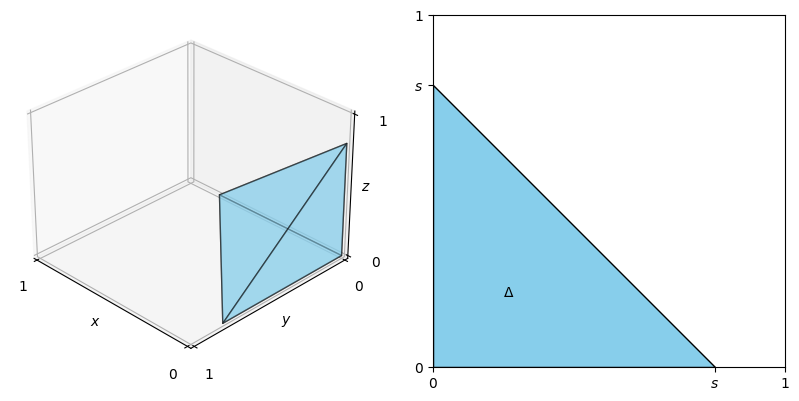
Therefore, $(1)$ is equivalent to $$ \begin{align*} & \iiint_Vg(x, y, z)dxdydz = \iint_\Delta dydx\int_0^{s - x - y}g(x, y, z)dz = \int_0^s\int_0^{s - x}\int_0^{s - x - y}g(x, y, z)dzdydx = 0. \tag{2} \end{align*} $$ $(2)$ indeed holds (see Case 1 in the code chunk below).

Case 2. $s \in (1, 2)$. In this case, the projection of $V$ onto the $x$-$y$ plane is a pentagon, which is a disjoint union of a triangle $\Delta = \{(x, y): x + y \leq s - 1, x, y \geq 0\}$ and two trapezoids $T_1, T_2$, where $$ \begin{align*} & T_1 = \{(x, y): s - 1 - x \leq y \leq 1, 0 \leq x \leq s - 1\}, \\ & T_2 = \{(x, y): 0 \leq y \leq s - x, s - 1 \leq x \leq 1\}. \end{align*} $$

The visualization of $V$, $\Delta$, $T_1$ and $T_2$ is shown in the figure below:

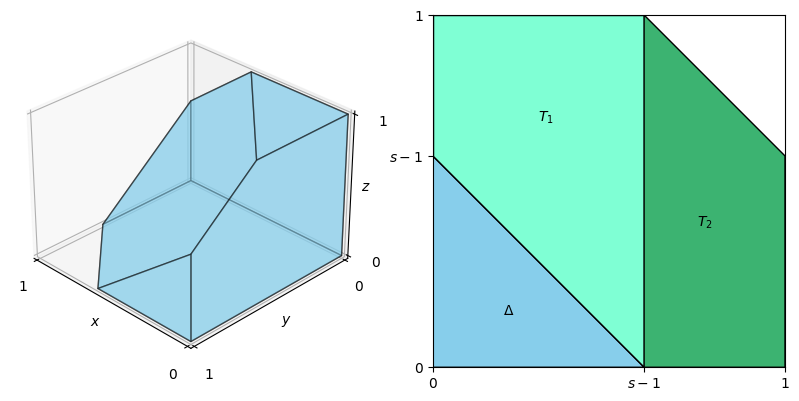
From the 3D plot of $V$, it is clear that on $\Delta$, the integration interval for $z$ is $[0, 1]$, and on $T_1 \cup T_2$, the integration interval for $z$ is $[0, s - x - y]$. Therefore, $(1)$ is equivalent to $$ \begin{align*} & \iint_{\Delta}dydx\int_0^1g(x, y, z)dz + \iint_{T_1 \cup T_2}dydx\int_0^{s - x - y}g(x, y, z)dz \\ =& \int_0^{s - 1}\int_0^{s - 1 - x}\int_0^1g(x, y, z)dzdx + \int_0^{s - 1}\int_{s - 1 - x}^1\int_0^{s - x - y}g(x, y, z)dzdydx + \int_{s - 1}^1\int_0^{s - x}\int_0^{s - x - y}g(x, y, z)dzdydx \\ =& 0.\tag{3} \end{align*} $$

$(3)$ indeed holds (see Case 2 in the code chunk below).

Case 3. $s \in [2, 3)$. In this case, the projection of $V$ onto the $x$-$y$ plane is the square $[0, 1] \times [0, 1]$, which is a disjoint union of a rectangle $R$, a trapezoid $T$ and a triangle $\Delta$, where $$ \begin{align*} & R = \{(x, y): 0 \leq y \leq 1, 0 \leq x \leq s - 2\}, \\ & T = \{(x, y): 0 \leq y \leq s - 1 - x, s - 2 \leq x \leq 1\}, \\ & \Delta = \{(x, y): s - 1 - x \leq y \leq 1, s - 2 \leq x \leq 1\}. \end{align*} $$

The visualization of $V$, $R$, $T$ and $\Delta$ is shown in the figure below:

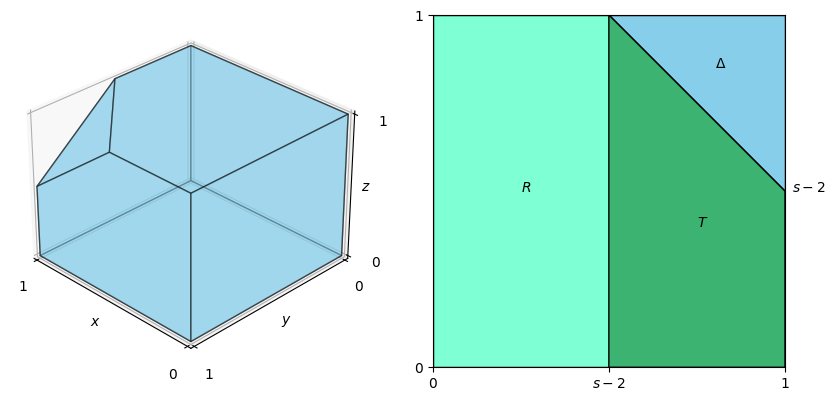
From the 3D plot of $V$, it is clear that on $R \cup T$, the integration interval for $z$ is $[0, 1]$, and on $\Delta$, the integration interval for $z$ is $[0, s - x - y]$. Therefore, $(1)$ is equivalent to prove $$ \begin{align*} & \iiint_Vg(x, y, z)dxdydz \\ =& \iint_{R \cup T}dydx\int_0^1g(x, y, z)dz + \iint_\Delta dydx\int_0^{s - x - y}g(x, y, z)dz \\ =& \int_0^{s - 2}\int_0^1\int_0^1g(x, y, z)dzdydx + \int_{s - 2}^1\int_0^{s - 1 - x}\int_0^1g(x, y, z)dzdydx + \int_{s - 2}^1\int_{s - 1 - x}^1\int_0^{s - x - y}g(x, y, z)dzdydx \\ =& 0. \tag{4} \end{align*} $$

$(4)$ indeed holds (see Case 3 in the code chunk below).

This completes the proof.

When the form of $E[Y \mid S]$ is unknown

If we are not told $E[Y \mid S] = \frac{S}{3}$, (in general) we can first determine $P(Y > y \mid S = s)$ using the approach as in this answer. Clearly we are still faced with several complicated triple integration problems and the analysis/tool in the proof above can be applied in a similar (but probably more verbose) manner. For this particular problem, because $(Y, S)$ has a non-degenerate density, this approach could be reduced to a more elementary method – that is, computing the conditional density $f(y \mid s)$ of $Y$ given $S$ directly using the formula $$ \begin{align*} f(y \mid s) = \frac{f(y, s)}{\int_0^s f(v, s)dv}, \quad 0 < y < s. \end{align*} $$

The joint density $f(y, s)$ can be determined by following a classical recipe in elementary probability, that is, by first evaluating the probability $F(y, s) := P(Y \leq y, S \leq s)$ then taking second-order partial derivative with respect to $s$ and $y$. As we have seen in the earlier proof, depending on where $s$ is located, the difficulty of computing $F(y, s)$ varies. Nevertheless, the key idea of converting a triple integration to an iterative integration by carefully gauging integration limits for $(x, y, z)$ stays the same. Below I illustrate this process for the (simplest) case $s \in (0, 1]$.

In this case, for $0 < y < s$, $F(y, s)$ is a triple integration of $f(u, v, w) = \frac{1}{3}(u + 2v + 3w)$ on the pentahedron $V = \{(u, v, w): u + v + w \leq s, 0 \leq u \leq 1, 0 \leq v \leq y\}$. Note that the projection of $V$ onto the $u$-$v$ plane is a trapezoid $T = \{(u, v): 0 \leq u \leq s - v, 0 \leq v \leq y\}$. See the figure below for the visualization of $V$ and $T$.

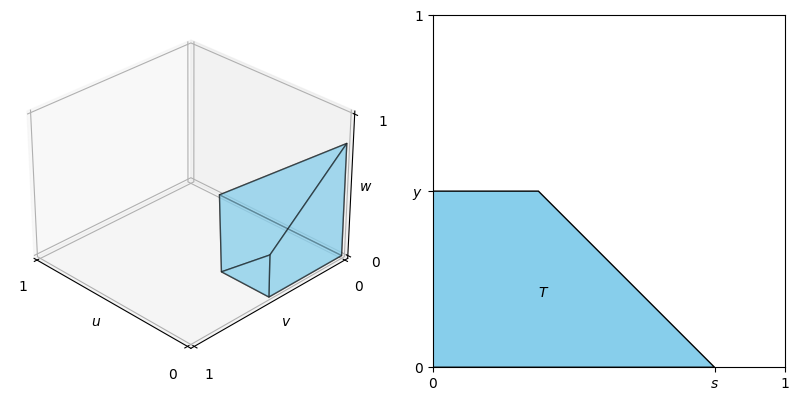
Therefore, $$ \begin{align*} & F(y, s) = \iiint_V f(u, v, w)dudvdw \\ =& \iint_Tdudv\int_0^{s - u - v}f(u, v, w)dw \\ =& \frac{1}{3}\int_0^y\int_0^{s - v}\int_0^{s - u - v}(u + 2v + 3w)dwdudv \\ =& \frac{2}{9}ys^3 - \frac{1}{6}s^2y^2 + \frac{1}{36}y^4. \end{align*} $$ The last integral is again obtained with the help of sympy. It then follows that $$ \begin{align*} f(y, s) = \frac{\partial^2 F(y, s)}{\partial y\partial s} = \frac{2}{3}s(s - y), \quad 0 < y < s. \end{align*} $$ whence $$ \begin{align*} f(y \mid s) = \frac{f(y, s)}{\int_0^s f(v, s)dv} = \frac{2}{s}\left(1 - \frac{y}{s}\right), \quad 0 < y < s. \end{align*} $$ Hence $$ \begin{align*} E[Y \mid S = s] = \int_0^syf(y \mid s)dy = \frac{2}{s}\int_0^s\left(y - \frac{y^2}{s}\right)dy = \frac{s}{3}, \end{align*} $$ as desired.

Python Code

from sympy import symbols, integrate, simplify
x, y, z, s = symbols('x y z s')
f = (2 * y - x - z) * (x + 2 * y + 3 * z)

def int_3D(il, iu, ml, mu, ol, ou):
    f_inner = integrate(f, (z, il, iu)) 
    f_middle = integrate(f_inner, (y, ml, mu))
    f_outer = integrate(f_middle, (x, ol, ou))

    res = simplify(f_outer)
    print("The result of the triple integral is: ", res)
    return res

# Case 1: 0 < s <= 1
res_c1 = int_3D(0, s - x - y, 0, s - x, 0, s)
# res_c1 = 0

# Case 2: 1 < s < 2
I1 = int_3D(0, 1, 0, s - 1 - x, 0, s - 1) 
# I1 = s**4/4 - s**3 + s**2 - 1/4
I2 = int_3D(0, s - x - y, s - 1 - x, 1, 0, s - 1) 
# I2 = -s**4/2 + 11*s**3/6 - 11*s**2/6 + 5*s/12 + 1/12
I3 = int_3D(0, s - x - y, 0, s - x, s - 1, 1) 
# I3 = s**4/4 - 5*s**3/6 + 5*s**2/6 - 5*s/12 + 1/6
res_c2 = simplify(I1 + I2 + I3)
# res_c2 = 0

# Case 3: 2 <= s < 3
I1 = int_3D(0, 1, 0, 1, 0, s - 2)
# I1 = -s**3/3 + s**2 + 4*s/3 - 4
I2 = int_3D(0, 1, 0, s - 1 - x, s - 2, 1)
# I2 = -s**4/4 + 7*s**3/3 - 13*s**2/2 + 14*s/3 + 7/4
I3 = int_3D(0, s - x - y, s - 1 - x, 1, s - 2, 1)
# I3 = s**4/4 - 2*s**3 + 11*s**2/2 - 6*s + 9/4
res_c3 = simplify(I1 + I2 + I3)
# res_c3 = 0